Sustainable Marine Structures

Flow Structures around a Sphere Attached to the Bottom of a Prismatic Sloshing Tank: Problem‑Oriented Basic Research

Murat Aksel

Department of Civil Engineering, Alanya Alaaddin Keykubat University, Alanya 07425, Antalya, Türkiye

Oral Yagci

Civil Engineering Department, Engineering Faculty, Aydin Adnan Menderes University, Aydin 09010, Türkiye

Manousos Valyrakis

Department of Civil Engineering, Aristotle University of Thessaloniki, Thessaloniki 54645, Greece

Veysel Sadan Ozgur Kirca

Civil Engineering Department, Istanbul Technical University, Istanbul 34555, Türkiye

DOI: https://doi.org/10.36956/sms.v6i2.1204

Received: 8 July 2024 | Revised: 9 August 2024 | Accepted: 15 September 2024 | Published Online: 22 September 2024

---

Abstract

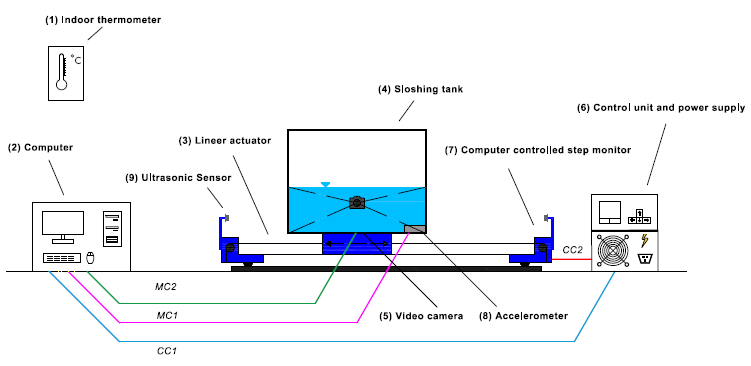
This study aimed to investigate the spatiotemporal variation of hydrodynamic variables around a sphere rigidly fixed to the bottom of a sloshing tank. The experimental measurement of the variations of dynamic variables around a body in a sloshing tank requires non-intrusive measurements that are usually expensive and sometimes inapplicable. Therefore, the numerical model could serve as a cost-effective tool for such problems. A two-stage analysis was conducted. In the first stage, an experimental study was carried out in a testing system comprising a water tank with uniaxial freedom of movement constructed on a monorail operated by a computer-controlled step motor. The primary objective of the experiments was to generate reliable data for calibrating the numerical model.

During the experiments, the tank's movements were recorded using an accelerometer and ultrasonic sensors with a sampling frequency of 200 Hz for each. The accelerometer and ultrasonic sensor data were used to impose the motion of the sloshing tank into a Reynolds-Averaged Navier-Stokes (RANS)-based numerical model. The video recordings, which comprised temporal fluctuations of the water surface, were used to calibrate the Model 1. Once the first numerical model was calibrated based on water surface level records using image processing methods, the second numerical model was constructed to accommodate a rigid spherical body with a 17 mm diameter connected to the bottom of the sloshing tank. The initial and boundary conditions used in the second numerical model were identical to those used in the first model to measure the spatiotemporal fluctuations of the surrounding spherical body's kinematic and dynamic variables, respectively. The findings revealed that sloshing motion exerts a significant impact on the boundary layer separation process around the sphere. It was also witnessed that the stage of the sloshing motion controls the temporal lag between the pressure, velocity and water surface level.

Keywords: Boundary Layer Separation; Drag Force; Particle Hydrodynamics; Sediment Transport; Sloshing Tank; Oscillatory Flow; Wake Region

---

References

[1] Brown, S., Nicholls, R.J., Woodroffe, C.D., et al., 2013. Sea-level rise impacts and responses: a global perspective. In: Finkl, C.W. (ed.). Coastal Hazards. Springer: Dordrecht, The Netherlands. pp. 117–149.

[2] Small, C., Nicholls, R.J., 2003. A global analysis of human settlement in coastal zones. Journal of Coastal Research. 19(3), 584–599.

[3] United Nations, 2017. Factsheet: people and oceans. The Ocean Conference; June 5–9, 2017; New York, USA. pp. 1–2.

[4] Globalization and World Cities, 2023. Globalization and World Cities Research Network. Available from: https://gawc.lboro.ac.uk/gawc-worlds/the-world-according-to-gawc/world-cities-2024/ (cited 31 May 2023).

[5] Neumann, B., Vafeidis, A.T., Zimmermann, J., et al., 2015. Future coastal population growth and exposure to sea-level rise and coastal flooding - a global assessment. Public Library of Science One. 10(3), e0118571.

[6] Bamber, J.L., Oppenheimer, M., Kopp, R.E., et al., 2019. Ice sheet contributions to future sea-level rise from structured expert judgment. Proceedings of the National Academy of Sciences. 116(23), 11195–11200.

[7] Nicholls, R.J., Marinova, N., Lowe, J.A., et al., 2011. Sea-level rise and its possible impacts given a ‘beyond 4°C world’ in the twenty-first century. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 369(1934), 161–181.

[8] Mohammed, A., 2019. Sustainable floating cities can offer solutions to climate change threats facing urban areas, deputy secretary-general tells first high-level meeting. Available from: https://press.un.org/en/2019/dsgsm1269.doc.htm (cited 31 May 2023).

[9] American Society of Civil Engineers, 2019. Future world vision: infrastructure reimagined. Available from: https://futureworldvision.org/ (cited 31 May 2023).

[10] Watanabe, E., Wang, C.M., Utsunomiya, T., et al., 2004. Very large floating structures: applications, analysis and design. 2004–02.

[11] Hadary, T., Martinez, J.G., Sella, I., et al., 2022. Eco-engineering for climate change - floating to the future. Proceedings of the Second World Conference on Floating Solutions, Rotterdam; October 27–29, 2020; Rotterdam, Netherlands (Rotterdam, NL). pp. 409–421.

[12] Wang, C.M., Watanabe, E., Utsunomiya, T., 2008. Very Large Floating Structures. Chemical Rubber Company Press: Boca Raton, Florida, USA. pp. 11.

[13] Bandrowski, T.J., 2015. Lily Pad Urbanism: Reimagining Seattle’s Floating Home Community [Master’s dissertation]. Seattle, WA: University of Washington. p. 11.

[14] Blanco, L.F.L., Hancco, R.W.M., 2020. Modeling and forecasting international tourism demand in Puno-Peru. Revista Brasileira de Pesquisa em Turismo. 14(1), 34–55.

[15] Lin, Z., 2007. Urban structure for the expanding metropolis: Kenzo Tange’s 1960 plan for Tokyo. Journal of Architectural and Planning Research. 24(2), 109–124.

[16] Cebada-Relea, A.J., Lopez, M., Aenlle, M., 2022. Time-domain numerical modelling of the connector forces in a modular pontoon floating breakwater under regular and irregular oblique waves. Ocean Engineering. 243, 110263.

[17] Ren, N., Zhang, C., Magee, A.R., et al., 2019. Hydrodynamic analysis of a modular multi-purpose floating structure system with different outermost connector types. Ocean Engineering. 176, 158–168.

[18] Gutierrez-Romero, J.E., Garcia-Espinosa, J., Servan-Camas, B., et al., 2016. Non-linear dynamic analysis of the response of moored floating structures. Marine Structures. 49, 116–137.

[19] Rahman, M.A., Mizutani, N., Kawasaki, K., 2006. Numerical modeling of dynamic responses and mooring forces of submerged floating breakwater. Coastal Engineering. 53(10), 799–815.

[20] Bouscasse, B., Colagrossi, A., Marrone, S., et al., 2013. Nonlinear water wave interaction with floating bodies in SPH. Journal of Fluids and Structures. 42, 112–129.

[21] Dominguez, J.M., Crespo, A.J., Hall, M., et al., 2019. SPH simulation of floating structures with moorings. Coastal Engineering. 153, 103560.

[22] Takabatake, H., 2015. A simplified analysis of rectangular floating plates subjected to moving loads. Ocean Engineering. 97, 37–47.

[23] Wang, S., 2023. Simplified analytical solutions to the yaw dynamics of modular floating structures. Ocean Engineering. 276, 114206.

[24] Wang, S., 2022. Analytical solutions for the dynamic analysis of a modular floating structure for urban expansion. Ocean Engineering. 266, 112878.

[25] Suzuki, H., Yoshida, K., 1996. Design flow and strategy for safety of very large floating structure. Proceedings of the International Workshop on Very Large Floating Structures; April 24–26, 1996; Hayama, Japan (Hayama, Kanagawa). pp. 21–27.

[26] Barltrop, N.D.P., 1998. Floating Structures: A Guide for Design and Analysis. Oilfield Publications Limited: Ledbury, UK. pp. 471–514.

[27] Vugts, J.H., 1968. The hydrodynamic coefficients for swaying, heaving, and rolling cylinders in a free surface. International Shipbuilding Progress. 15(167), 251–276.

[28] C. E. Brennen, 1982. A review of added mass and fluid inertial forces. 82.010, January 1982.

[29] United States Army Corps of Engineers, 2012. Coastal Engineering Manual. USACE: Washington, DC, USA. Part II, Chapter 1, p. 13.

[30] Faltinsen, O., 1993. Sea Loads on Ships and Offshore Structures. Cambridge University Press: Cambridge, UK. pp. 37–101.

[31] Goda, Y., 2000. Random Seas and Design of Maritime Structures, 2nd ed. World Scientific Publishing Company: Singapore. pp. 12–44.

[32] Nakajima, T., Saito, Y., Umeyama, M., 2022. A study on stability of floating architecture and its design methodology. Proceedings of the Second World Conference on Floating Solutions, Rotterdam; October 27–29, 2020; Rotterdam, Netherlands (Rotterdam, NL). pp. 273–296.

[33] Xu, H., Neng, P., Yang, F., 2019. Motion response analysis of mining vessel based on ANSYS/AQWA. Journal of Physics: Conference Series. 1300(1), 012010.

[34] Wang, G., Goldfeld, Y., Drimer, N., 2019. Expanding coastal cities - Proof of feasibility for modular floating structures (MFS). Journal of Cleaner Production. 222, 520–538.

[35] Wang, G., Drimer, N., Goldfeld, Y., 2020. Modular floating structures (MFS) for offshore dwelling a hydrodynamic analysis in the frequency domain. Ocean Engineering. 216, 107996.

[36] Chakrabarti, S., 2001. Empirical calculation of roll damping for ships and barges. Ocean Engineering. 28(7), 915-932.

[37] ISO 10137:2007. 2007. Bases for design of structures - Serviceability of buildings and walkways against vibrations.

[38] Boggs, D., 1997. Acceleration Indexes for Human Comfort in Tall Buildings - Peak or RMS?. Council on Tall Buildings and Urban Habitat Monograph. 13, 1–21.